Линия в искусстве

Центр лабиринта – что там?

Работа Тони Пекораро

Почему в мистерии лабиринта все стремятся достигнуть центра и готовы для достижения этой цели проходить долгий путь?

Вероятные ответы на символическом, смысловом уровне:

в центре лабиринта – происходит вознесение, после того, как ты прожил жизнь от рождения до смерти (этот смысл сохранен индейцами Центральной Америки);
там находится портал, врата в другие измерения, и лишь тот, кто добрался до Центра лабиринта, способен ими воспользоваться;
там сидит чудовище (этот вариант донесла до нас греческая мифология), но это касается хаотического лабиринта. Здесь логично предположить, что человека поджидает страшная встреча вовсе не в центре, а по дороге, где именно «чудовище» мешает ему достигнуть центра, рыская по лабиринту.

Греческий Минотавр — это символ подсознания, страха и тьмы, когда «сон разума порождает чудовищ». Явно это было показано в фильме «Кубок Огня» про Гарри Поттера, когда на последнем испытании – большинство волшебников, оказавшись в лабиринте, менялись совсем не в лучшую сторону.

Тогда, лабиринт выступает моделью человеческого мозга, его психики – где:

Изображение шишковидной железы в различных духовных культурах мира

в центре превозносимая всеми духовными школами Шишковидная железа, отвечающая за нашу связь с непознанным (нагуалем), Высшими мирами и сущностями;
а до центра, вокруг него – программы обычного мира (матрицы), а также неосвоенный или засасывающий опыт прошлых воплощений (карма) — через которые сложно прорваться к истинному восприятию, к чистому Видению.

Кто такие кельты

Кельтские узоры – наследие великой цивилизации, еще в седьмом веке до н. э. покинувшей континентальную Европу и постепенно обособившейся (или обосновавшейся) на островах, которые сейчас входят в состав Великобритании.

Благодаря богатым представителям народа, искусство успешно развивалось под их покровительством, а значение символов было многогранным.

Оно представляло историю, религию и социальную подоплеку тогдашней жизни, одновременно украшая ее и выполняя своеобразную просветительскую функцию. Загадочные, таинственные и красивые, они стали частью современной культуры.

Трехмерный

Коническая спираль со спиралью Архимеда в виде плана этажа

Конические спирали

Икс=р(φ)потому что⁡φ ,у=р(φ)грех⁡φ{ Displaystyle х = р ( varphi) соз varphi , qquad y = r ( varphi) sin varphi}

задана, то можно добавить третью координату z(φ){ Displaystyle г ( varphi)}, такая, что кривая пространства теперь лежит на конус с уравнением м(Икс2+у2)=(z−z)2 , м>{ Displaystyle ; м (х ^ {2} + y ^ {2}) = (z-z_ {0}) ^ {2} , m> 0 ;}:

Икс=р(φ)потому что⁡φ ,у=р(φ)грех⁡φ ,z=z0+мр(φ) .{ displaystyle x = r ( varphi) cos varphi , qquad y = r ( varphi) sin varphi , qquad color {red} {z = z_ {0} + mr ( varphi )} .}

Спирали на основе этой процедуры называются конические спирали.

Пример

Начиная с архимедова спираль р(φ)=аφ{ Displaystyle ; г ( varphi) = а varphi ;} получается коническая спираль (см. схему)

Икс=аφпотому что⁡φ ,у=аφгрех⁡φ ,z=z+маφ ,φ≥ .{ displaystyle x = a varphi cos varphi , qquad y = a varphi sin varphi , qquad z = z_ {0} + ma varphi , quad varphi geq 0 . }

Сферическая спираль с c=8{ displaystyle c = 8}

Сферические спирали

Если один представляет сферу радиуса р{ displaystyle r} к:

Икс=р⋅грех⁡θ⋅потому что⁡φу=р⋅грех⁡θ⋅грех⁡φz=р⋅потому что⁡θ{ displaystyle { begin {array} {cll} x & = & r cdot sin theta cdot cos varphi y & = & r cdot sin theta cdot sin varphi z & = & r cdot cos theta end {array}}}

Икс=р⋅грех⁡θ⋅потому что⁡cθу=р⋅грех⁡θ⋅грех⁡cθz=р⋅потому что⁡θ0≤θ≤π .{ displaystyle { begin {array} {cll} x & = & r cdot sin theta cdot cos { color {red} c theta} y & = & r cdot sin theta cdot sin { color {красный} c theta} z & = & r cdot cos theta qquad qquad 0 leq theta leq pi . end {array}}}

Паппу были известны и сферические спирали.

Замечание: а линия румба является нет сферическая спираль в этом смысле.

А линия румба (также известная как локсодромия или «сферическая спираль») — кривая на сфере, очерченная кораблем с постоянной несущий (например, путешествие из одного столб к другому, сохраняя фиксированный угол с уважением к меридианы ). Локсодрома имеет бесконечный количество революции, причем расстояние между ними уменьшается по мере приближения кривой к любому из полюсов, в отличие от Архимедова спираль который поддерживает равномерный межстрочный интервал независимо от радиуса.

Стрел(к)а

Последние два тысячелетия мы используем стрелку, чтобы показать направление движения. Но изначально ее понимали в первую очередь как материальный объект — оружие для охоты и защиты от врага. Это изменилось только в XIX веке, с приходом промышленной революции.

До того как появилась стрелка, направление показывали с помощью следа ноги, повернутого в нужную сторону. Такой рисунок вместе с изображением женского лица нашли на мостовой древнегреческого города Эфеса — это был указатель, как добраться до местного борделя.

Многие историки считают, что символическим значением стрелу наделили индейцы. Они почитали ее как символ жизни, потому что с помощью стрел защищались от диких животных и враждебных племен.

В зависимости от направления наконечника и количества стрел значение менялось. Вправо — защита, влево — отгон злых духов, вниз — мир. Две горизонтальные стрелки, направленные в разные стороны, — война, а перекрещенные — дружба.

В других культурах стрела тоже служила разного рода символом. Древние греки и римляне, например, связывали ее как со сражениями (богиня охоты Артемида почти не расставалась с луком и стрелами), так и с любовью (вспомни главное оружие Купидона). У индусов лук и стрелы считались и считаются символом не только физической, но и внутренней силы — храбрости, концентрации и острого ума.

Adventure-компания Go Ape своих клиентов стрелять из лука не учит, зато катает на веревочных тросах по разным живописным местам. Но стрелку в логотипе они все-таки спрятали:

Бесконечность в глубине отрезка

Совсем другой подход к кривым предложил великий французский математик Мари Энмон Камиль Жордан. Что если мы возьмем все точки отрезка и с помощью некоторого отображения перенесем их в пространство? Представьте, что наш отрезок сделан из проволоки, которую можно гнуть, вытягивать и сжимать. С помощью сжатия и вытягивания мы можем добиться изменения длины нашего отрезка, а с помощью сгибания — изменения его формы. Если же строго, то жордановой дугой называется образ непрерывного вложения отрезка в пространство: то есть разные точки отрезка обязательно перейдут в разные точки кривой. Можно представить, что отрезок у нас — временной, скажем, от начала работы секундомера до конца его работы. Тогда каждую секунду мы переводим в какое-то положение точки.

Жордановой замкнутой кривой называют образ непрерывного вложения окружности в пространство (из накладываемых требований следует, что окружность обязательно перейдет в некоторую замкнутую линию).

И хотя концепт жордановой кривой кажется достаточно простым, с его помощью можно получить весьма парадоксальные результаты.

Горизонталь или вертикаль

И еще кусочек. Разные композиции вызывают в зрителе разные эмоции. Ваша картина может быть как бы приплюснутой, горизонтальной. Это вызывает чувство спокойствия, уюта, неизменности.

Вертикаль, например, готический собор, навевает мысли об устремлении вверх, преодолении трудностей, стремлении к идеалам. Диагональ добавляет движение, как дорога уходящая вдаль. И есть ломаные, непрямые линии.

Природа всегда плавная, вы не найдете веточку, которая бы росла под прямым углом, или изломанную линию роста деревьев. Нет, только плавные, закругленные линии. Если же рисуете не природу, а, например, битву или городской пейзаж, то изломов не избежать. Ломаные линии дают картине жизнь, движение.

Как символ

Спиралевидная форма была найдена в Мезин, Украина, как часть декоративного объекта 10 000 г. до н. э.[нужна цитата ]

Чаша на подставке, Сосуд на подставке и Амфора. Энеолит, Культура Кукутень, 4300-4000 гг. До н.э. Нашел в Scânteia, Яссы, Румыния. Собрана Национальным музейным комплексом Молдавии.

В Ньюгрейндж входная плита

Этот Петроглиф с вырезанной на нем спиральной фигурой. Хохокамс, а Коренной американец племя более 1000 лет назад.

Спираль и тройная спираль мотив — это Неолит символ в Европе (Мегалитические храмы Мальты ). В кельтская Символ тройной спирали на самом деле является докельтским символом. Он высечен в скале каменной ромбовидной формы возле главного входа в доисторический Ньюгрейндж памятник в Графство Мит, Ирландия. Ньюгрейндж был построен около 3200 г. до н.э., до появления кельтов, а тройные спирали были вырезаны по крайней мере за 2500 лет до того, как кельты достигли Ирландии, но уже давно вошли в кельтскую культуру. В трискелион символ, состоящий из трех связанных спиралей или трех изогнутых человеческих ног, появляется во многих ранних культурах, в том числе Микенский сосуды, чеканка в Lycia, на статеры из Памфилия (в Аспендос, 370–333 до н.э.) и Писидия, а также на геральдический герб на воинских щитах, изображенных на греческой керамике.

Спирали можно найти в доколумбовом искусстве Латинской и Центральной Америки. Более 1400 петроглифы (наскальные рисунки) в Las Plazuelas, Гуанахуато Мексика, датируемые 750–1200 годами нашей эры, преимущественно изображают спирали, точечные фигуры и масштабные модели. В Колумбии фигуры, похожие на обезьян, лягушек и ящериц, изображенные на петроглифах или в виде золотых подношений, часто содержат спирали, например, на ладонях. В Нижней Центральной Америке спирали вместе с кругами, волнистыми линиями, крестами и точками являются универсальными символами петроглифов. Спирали также можно встретить среди линии Наска в прибрежной пустыне Перу, датируемой с 200 г. до н.э. по 500 г. н.э. В геоглифы исчисляются тысячами и изображают животных, растения и геометрические мотивы, в том числе спирали.

Спиральные формы, в том числе свастика, трискеле и т. д., часто интерпретировались как солнечные символы.[нужна цитата ]Черепица, относящаяся к династия Тан с этим символом были найдены к западу от древнего города Чанъань (современный Сиань).[нужна цитата ][год нужен ]

Спирали также являются символом гипноз, вытекающие из клише людей и героев мультфильмов, которые загипнотизированы, глядя во вращающуюся спираль (например, Каа в Дисней Книга джунглей ). Они также используются как символ головокружение, где глаза мультипликационного персонажа, особенно в аниме и манга, превратятся в спирали, чтобы показать, что у них головокружение или ошеломление. Спираль также встречается в таких небольших структурах, как двойная спираль из ДНК и размером с галактика. Из-за этого частого естественного явления спираль является официальным символом Мировое пантеистическое движение.Спираль также является символом диалектика процесс и Диалектический монизм.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество

Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней

Узоры в вязании и плетении

Если рисунок вплетен в вязание, то уместно использовать основные цвета древних кельтов. Это, как правило, зеленый, белый или красный, но не черный. Если вы решили использовать древний орнамент и ищите способ как завязать, то прежде всего нужно изучить фото.

Узел для браслета и сережек

Пошаговое выполнение браслета на руку может выглядеть так, как показано на фото 1.

А пошагово выполненный узел на женские серьги – следующим образом.

Кельтская коса

Это одна из самых популярных и распространенных схем в вязании, которую нужно вязать спицами по определенной схеме. Ее характерная особенность заключается в том, что она намного эффектней смотрится из толстых ниток.

В принципе, годится и любая пряжа (хлопковая и шерстяная нить, синтетика, нанизанный на нитку бисер, но считается, что определенное значение она приобретает только если связана из натурального сырья. Примерная схема выглядит так, как на фото 2.

Нужной ширины можно добиться просто кратно увеличивая число лицевых и изнаночных петель. Узор кельтская косичка, в современном рукоделии всегда актуален, и находится постоянно в числе модных трендов.

Его можно использовать, ничего не опасаясь, потому что многие поколения вязальщиц создавали индивидуальные схемы, видоизменяли узор и количество петель, и осталась только имитация некогда значимого символа, декоративный орнамент без особой смысловой нагрузки.

Кельтские узоры, значением которых стали интересоваться еще в незапамятные времена, а потом попросту позаимствовали в декоративных целях – это целая книга, которую невозможно прочитать полностью из-за безвозвратно утраченных знаний.

Во всем мире есть поклонники этих таинственных знаков с сакральным и глубоким значением. Они убеждены, что им удалось познать скрытые тайны. Но по-настоящему их могли растолковать только сами древние кельты, цивилизация которых осталась только в виде неповторимых и загадочных орнаментов.

Надеюсь из нашей публикации вы почерпнули много нового. Рекомендуйте наши статьи своим друзьям в соцсетях и подписывайтесь на обновления нашего блога!

Спираль

А вот и один из самых простых в исполнении символов, но при этом обладающий мощным «подтекстом» и энергией. Встречайте, спираль)

Принцип спирали часто встречается в природе — это галактики, водовороты и смерчи, раковины моллюсков, молекулы ДНК. Это символ, который был широко распространен еще на заре человечества. Нарисованная по часовой стрелке, священная спираль служит для того, чтобы привлекать вещи или явления и символизирует жизнь; нарисованная против часовой стрелки, священная спираль разрушает и символизирует смерть.

Спираль — символ познания себя, внутреннего путешествия и погружения, ведь если мы не познаем себя, то не можем надеяться на познание окружающего мира.

Подобно кругу, спираль связывают с образом бесконечности. Также спираль воплощает идеи развития и непрерывности космических ритмов.

Спираль — образ лабиринта, в котором центр символизирует семя духовной жизни, ее смысл. Иными словами, речь идет о втором рождении, инициации человека.

Спираль представляет собой образ энергии Кундалини, которая находится в каждом человеке в свернутом состоянии (Кундалини переводится с санскрита как «свернутая», «свитая») и может быть пробуждена. Пробуждаясь, Кундалини объединяет все чакры человека и дает ему Йогу, т.е. «союз» с энергией, создавшей весь мир. Это живая энергия, преобразовывающая, исцеляющая сила, предназначенная для достижения человеком своего предназначения. Пробудить ее — большое благо.

Спираль ассоциируется также с прядением и тканием паутины жизни Богиней-Матерью, которая распоряжается судьбами и ткет завесы иллюзий.

Символ бесконечности

Научное название лежащей на боку восьмерки, которую мы привыкли считать символом бесконечности, — лемниската (от лат. lemniscus — лента.). Его создателем считается английский математик Джон Уоллис. Он впервые использовал этот знак в своем трактате «О конических сечениях» в 1655 году.

По одной версии, Уоллис вдохновлялся римским символом CIƆ или CƆ, который означал цифру 1000, а иногда просто «много» или «бесчисленное множество». По другой — это вариация греческого символа омега (ω). По кривой, у которой нет ни начала, ни конца, можно двигаться бесконечно, так что ∞ стал идеальным символом этой концепции.

В мистицизме бесконечность символизирует уроборос (от древнегреч. οὐρά — хвост, βορά — пища). Это змей или дракон, пожирающий собственный хвост. Его изображали как в виде круга, так и в виде восьмерки.

Уроборос встречается во многих культурах: греческой, римской, египетской, индийской, китайской, скандинавской. В основном его использовали в контексте жизни и смерти — рисовали на стенах гробниц и в погребальных текстах. Уроборос символизирует бесконечный цикл обновления Вселенной и перерождение. Он как бы показывает: из смерти появляется жизнь, из разрушения рождается творение.

В работу дизайн-студии интерьера Bonito Designs концепция обновления вполне вписывается. А лемниската — в логотип. В паре с лестницей она означает движение вперед, вверх, в будущее, где возможности безграничны:

Гладкость

Еще одним свойством, характеризующим кривые, является гладкость. Хотя смысл слова интуитивно понятен, задать ее математически не совсем элементарно. Мы хотим, чтобы у кривой не было углов, заострений, клювов и т. п.

Хороший пример гладкой кривой — синусоида:

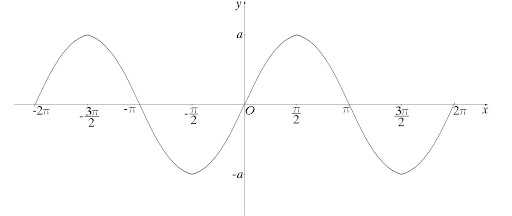
А вот пример негладкой кривой:

Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.

В курсе начал анализа доказывается, что такая касательная неразрывно связана с производной функции, график которой образует нашу кривую: более конкретно — тангенс угла наклона касательной (по отношению к положительному направлению оси Ox) равен значению производной функции в точке касания.

Эта связь позволяет нам четко определить гладкость функции. Чтобы функция называлась гладкой (и, следовательно, ее график был гладкой кривой), необходимо, чтобы, во-первых, эта функция была непрерывной, во-вторых, ее производная должна существовать и быть непрерывной.

Может быть интересно

Кажется, что гладкость — довольно естественное требование к кривой. Это ощущение привело к тому, что в 1806 году Андре-Мари Ампер выдвинул гипотезу о том, что любая функция всюду, за исключением отдельных, «исключительных и изолированных» точек, имеет производную в этих точках.

Позднее гипотеза была разрушена. Первый контрпример следует атрибутировать, по-видимому, Бернхарду Риману. Более простой и широко известный контрпример был построен Ван дер Варденом позднее, в 1930 году. Но наибольшей известностью пользуется функция Вейерштрасса, выраженная формулой:

здесь a — любое нечетное число кроме единицы, b — число от нуля до единицы, а большая греческая cигма обозначает суммирование. Функция оказывается непрерывной для всех вещественных х, но при ряде условий на a и b очень негладкой:

Перспектива и другие художественные тонкости

Не забывайте, пожалуйста, про восприятие объема и картины в целом. Правильно передавайте перспективу, то есть отношение объектов на разном отдалении от зрителя. Помните, что стоящий человек закрывает головой горизонт, имеет живую позу и скорее всего идет наискосок, а не вдоль линии горизонта.

Но детально это все мы рассмотрим в других статьях. А вы сейчас постарайтесь передать картинку такой, какой вы ее видите. Я бы рекомендовала на начальных этапах делать фотографию и уже с нее рисовать. Так вы увидите правильное расположение ваших предметов на плоскости.

Но и модель убирать не стоит, ведь что-то лучше видно в объеме! Постарайтесь рисовать при естественном или хорошем искусственном освещении, чтобы вы видели правильные цвета ваших моделей.

И на сегодня все, сходите в музей, чтобы еще раз увидеть все варианты композиций и приступайте к работе. Напишите, какие еще темы интересны в отношении изобразительного искусства. Полезна ли была эта статья для рисунка и для фотографии? Оставьте свой комментарий.

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

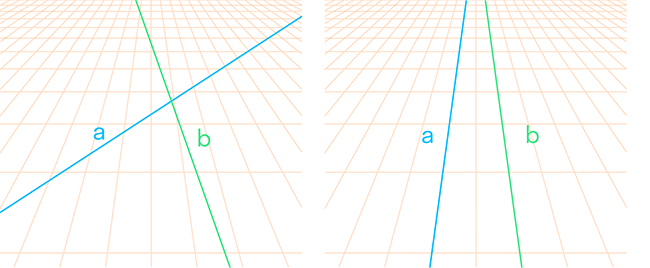
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

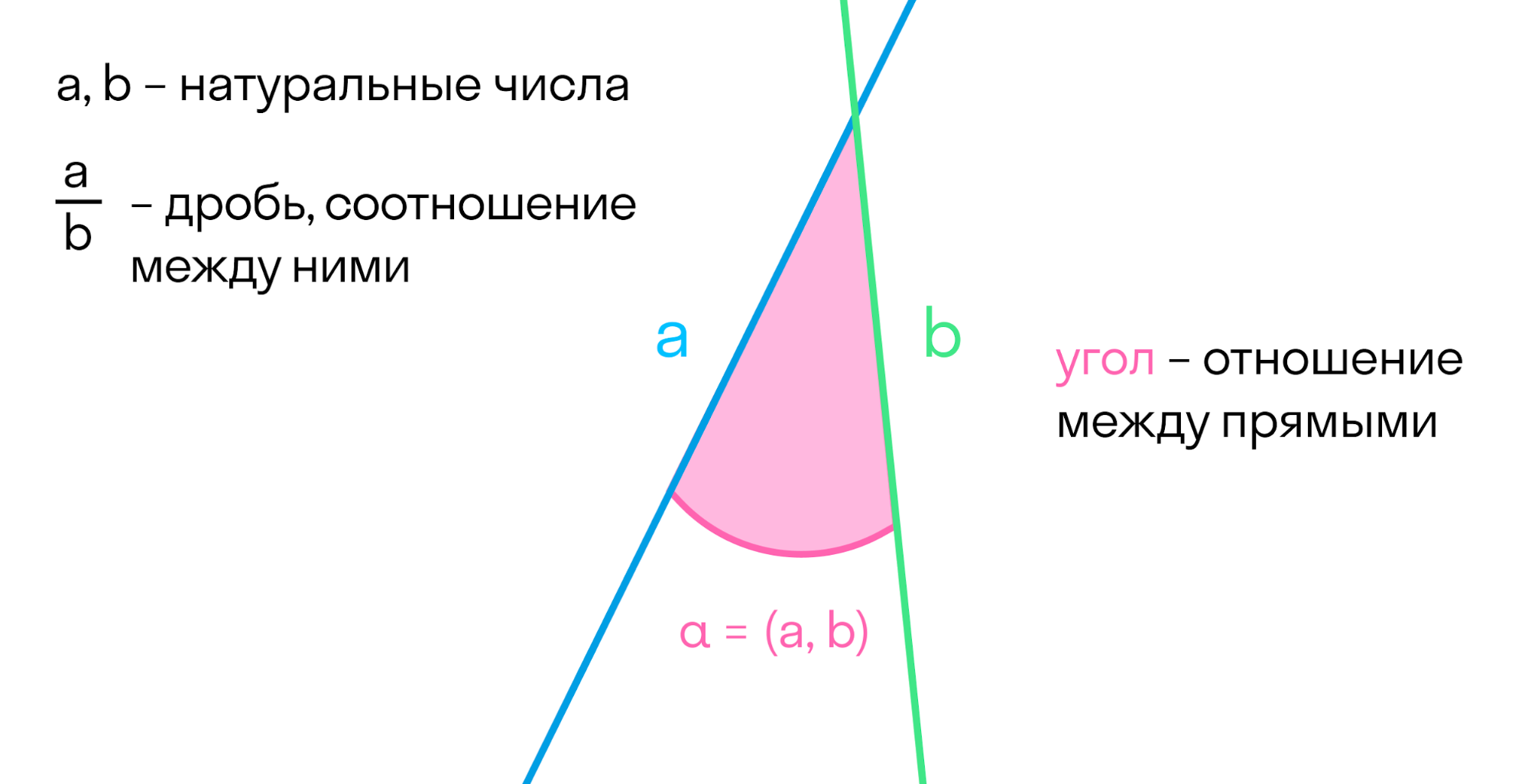
Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

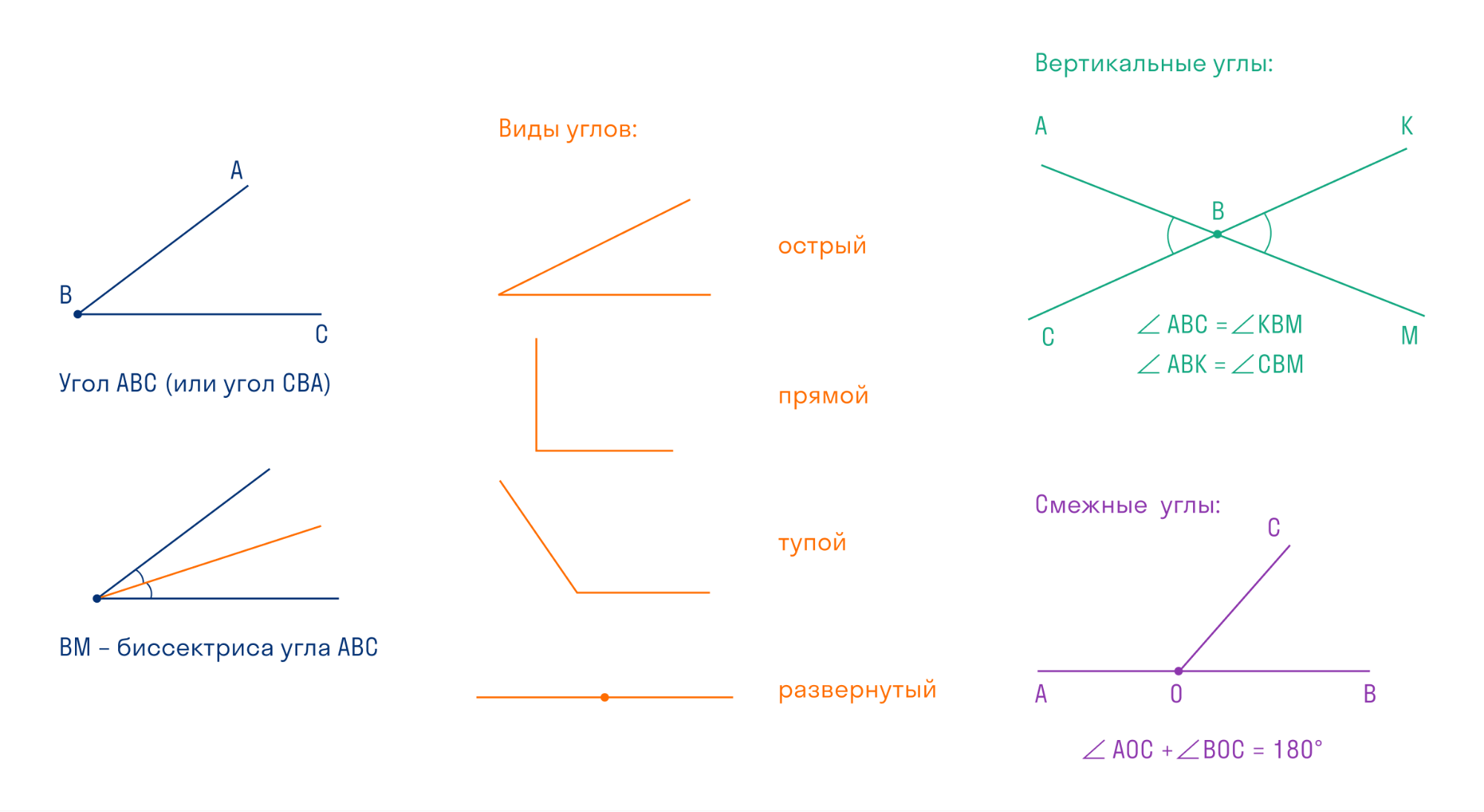
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

Есть разные виды углов, выделим самые часто встречающиеся:

Если градусная мера угла меньше 90° — угол острый.
Если градусная мера угла равна 90° — угол прямой.
Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
Если градусная мера угла равна 180° — угол развернутый.

Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

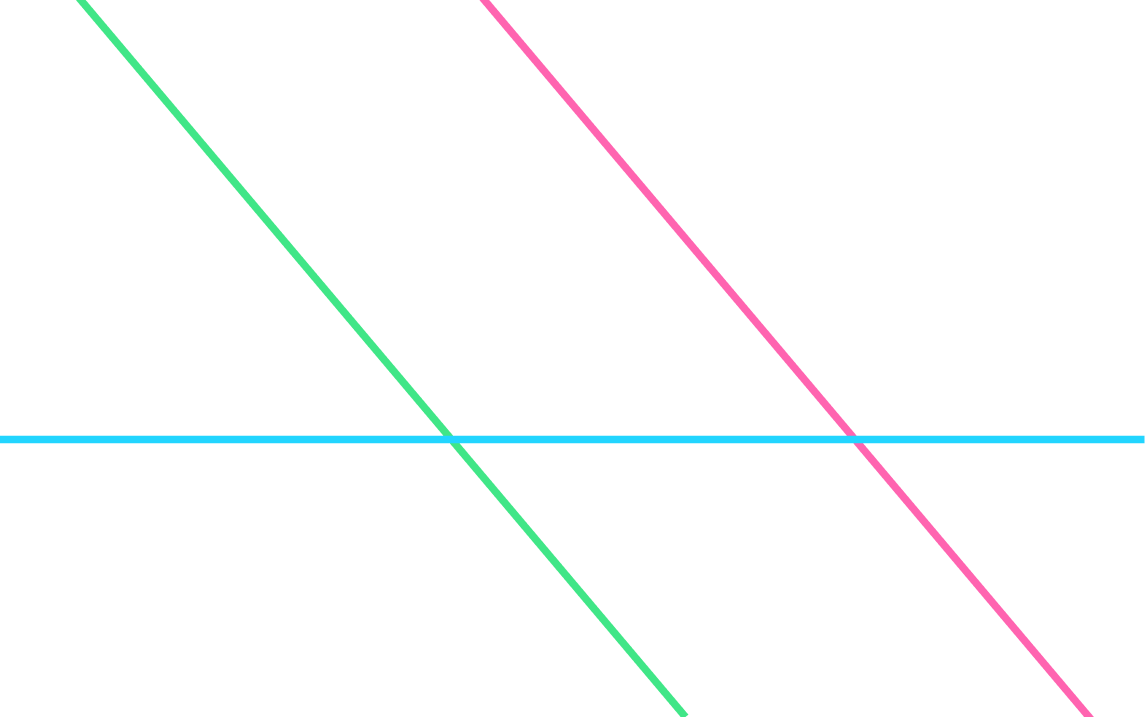
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

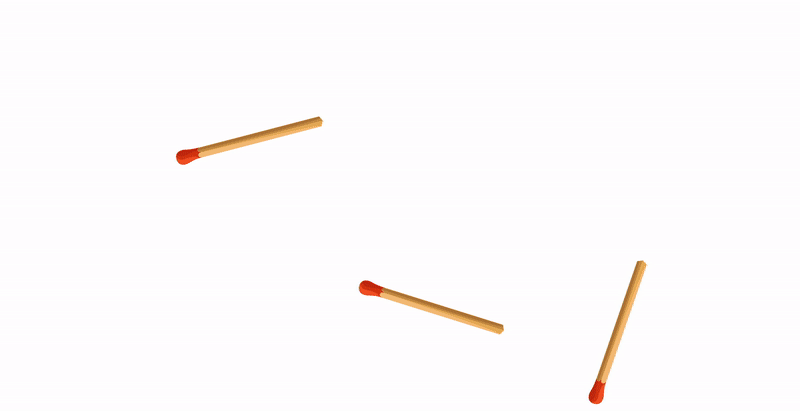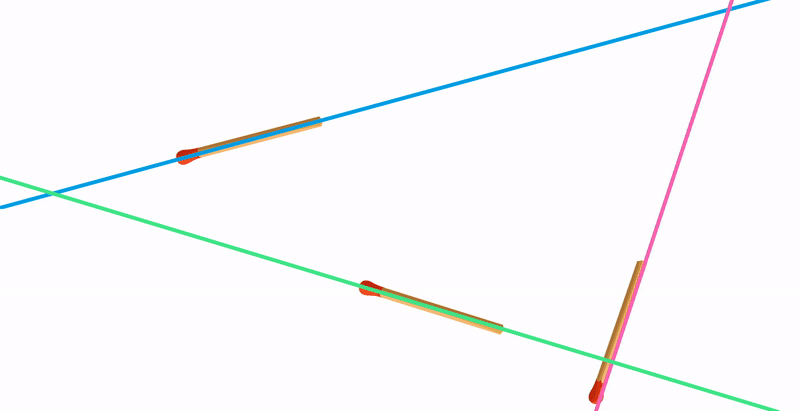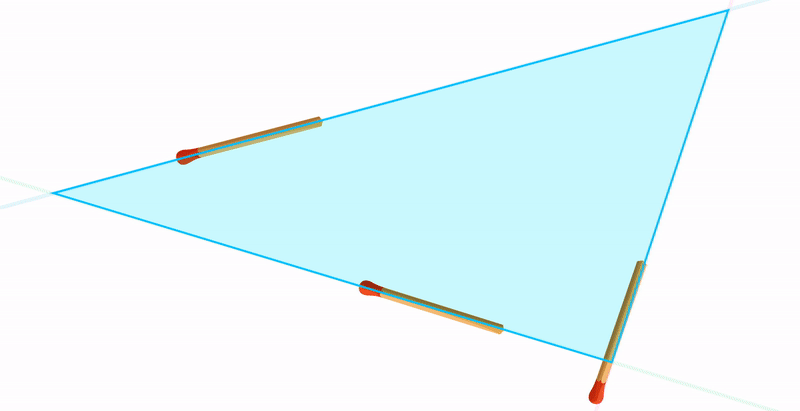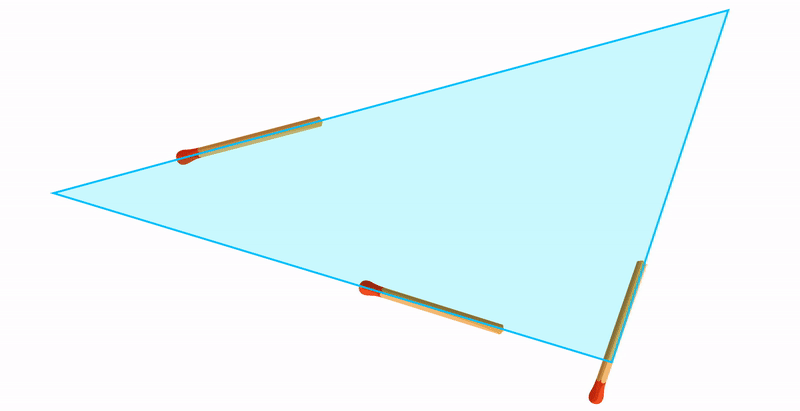
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Записаться на интенсив

Греция: длина без ширины

Древние греки подошли к вопросу более строго. В «Началах» Евклида возникают определения (впрочем, зачастую носящие скорее описательный характер — на них, например, не ссылаются далее) линии, прямой линии, точки. Выглядят они, мягко говоря, несовременно:

Определение 1.1. Точка — это то, часть чего есть ничто.

Определение 1.2. Линия — это длина без ширины.

Определение 1.3. Концы линий — это точки.

Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней. (Или: Прямая линия есть та, которая равно лежит на всех своих точках.)

Первое из этих определений можно при желании трактовать в духе теории множеств, третье, по-видимому, намекает, что линии у нас априори конечные. Второе можно трактовать описательно, что касается четвертого, то мнения сильно расходятся.

Несколько иная, хотя местами и похожая ситуация возникает в труде, традиционно приписываемом Герону, — «Определение понятий геометрии» (но в статье W. R. Knorr, ‘Arithmêtikê stoicheiôsis’: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180–192 приводятся аргументы в пользу принадлежности его Диофанту):

Последнее определение довольно явно отсылает нас к кратчайшему расстоянию между двумя точками.

В наиболее известных трудах древних греков рассматриваются главным образом прямые линии. Хотя в некоторых трудах встречаются и иные известные им линии.

Аполлоний Пергский, один из трех великих геометров Античности (вместе с Евклидом и Архимедом), занимался коническими сечениями. Об их существовании знали и до него, однако именно он дал им названия, закрепившиеся в науке, — эллипс, гипербола, парабола.